Le hashing consistant a été introduit en 1997 par le papier Consistent Hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web de Karger D., Lehman E., Leighton T., Panigrahy R., Levine M., Lewin, D. Le hashing consistant est aujourd’hui une brique fondatrice et incontournable à beaucoup de technologies dites distribuées. Comprendre ce qu’est le hashing consistant permet d’appréhender ces technos et d’en imaginer le fonctionnement. Ce billet a pour objectif de vulgariser le concept de hashing consistant.
A la fin des années 90, les sites internet populaires commencent à crouler sous les requêtes des internautes.
Chaque document servi est identifié par une requête unique, genre http://www.altavista.fr/search?q=netscape.
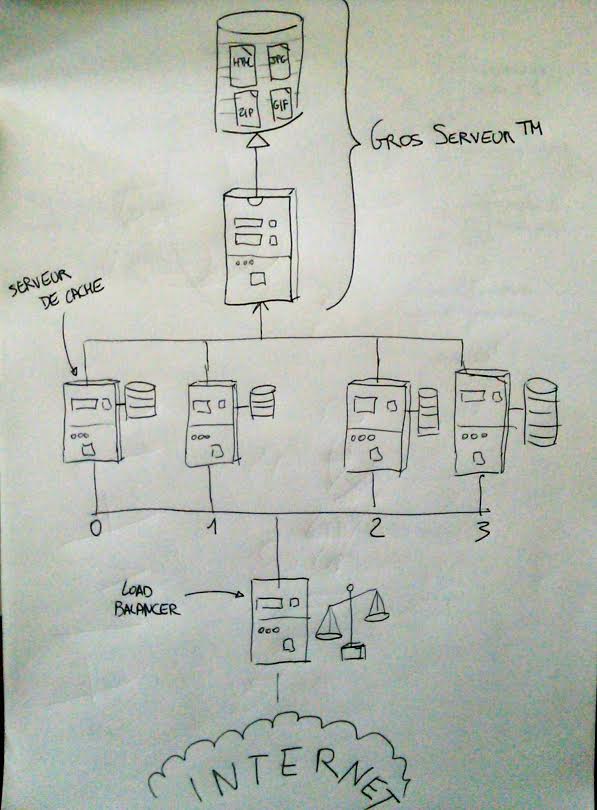
Le gros serveur™ reçoit la requête, fait un calcul coûteux avant de servir un document à l’internaute.
Et quand le serveur reçoit 15000 requêtes en même temps …
____ _ _
| __ ) ___ ___ _ __ ___ | | |
| _ \ / _ \ / _ \| '_ ` _ \ | | |
| |_) | (_) | (_) | | | | | | |_|_|
|____/ \___/ \___/|_| |_| |_| (_|_)
On se rend compte que :
- certaines url sont plus sollicitées que d’autres et qu’il est dommage de faire le même calcul plusieurs fois
- le gros serveur est taillé pour les calculs et pas pour la distribution de contenu
La solution consiste à mettre un serveur de cache en frontal. Le serveur de cache a deux possibilités. Soit il possède localement le résultat pour l’URL qu’on lui demande (en mémoire ou sur disque), dans ce cas il répond instantanément, soit il n’a pas le résultat alors il le demande au gros serveur, répond, et le stocke localement. Avec ça, on a résolu le problème du calcul redondant et déporté la responsabilité de servir du contenu. Mais quand le serveur de cache reçoit 30000 requêtes en même temps …
____ _ _
| __ ) ___ ___ _ __ ___ | | |
| _ \ / _ \ / _ \| '_ ` _ \ | | |
| |_) | (_) | (_) | | | | | | |_|_|
|____/ \___/ \___/|_| |_| |_| (_|_)
Alors on multiplie les serveurs de cache et on ajoute un load balancer. Le load balancer reçoit toutes les URLs et les répartit aux serveurs de cache. Et voici, le schéma qu’il faut mettre en forme avec PowerPoint :
L’algorithme magique de répartition d’une URL à un serveur de cache est le suivant :
serveur-de-cache = hash(URL) modulo nb-de-serveur-de-cache
Simplissime ! Pour une URL donnée, on sollicite toujours le même serveur de cache, et on sollicite le moins possible le gros serveur™. On a résolu pour de bon le problème de mise à l’échelle (scalabilité). On attend le prix Nobel.
Mais qu’est ce qui ce passe si on débranche l’un des serveurs de cache ? Et bien, nombre-de-serveur-de-cache est
décrémenté, et l’algorithme magique ne distribue
plus du tout les URLs aux mêmes serveurs de cache. Cela signifie que pendant un moment, les serveurs de cache sollicitent
systématiquement le gros serveur™ et …
____ _ _
| __ ) ___ ___ _ __ ___ | | |
| _ \ / _ \ / _ \| '_ ` _ \ | | |
| |_) | (_) | (_) | | | | | | |_|_|
|____/ \___/ \___/|_| |_| |_| (_|_)
Et c’est à ce moment que je commence à vous parler des algorithmes de hashage consistants, et que je plagie Wikipedia. La façon la plus simple de saisir le concept est d’utiliser l’allégorie du cercle. Sur un cercle, on peut apposer n’importe quel serveur de cache par la formule magique :
angle-du-cercle = hash(serveur-de-cache) modulo 360
On peut également apposer n’importe qu’elle URL par la formule magique :
angle-du-cercle = hash(URL) modulo 360
Ce qui pourrait donner un cercle du genre :
Maintenant mettons-nous à la place du load-balancer. Comment trouver le serveur de cache responsable de l’URL
http://www.altavista.fr/search?q=netscape ?
1) On calcule la position de l’URL sur le cercle, disons 73°
2) Connaissant la position de tous les serveurs de cache sur le cercle, on recherche celui qui est le plus proche l’URL tout en étant plus loin selon le sens horaire, soit le serveur de cache n°2.
On a donc pour le moment les correspondances suivantes :
- Serveur de cache n°1 :
http://www.altavista.fr/search?q=gopher - Serveur de cache n°2 :
http://www.altavista.fr/search?q=netscape - Serveur de cache n°3 :
http://www.altavista.fr/search?q=operaethttp://www.altavista.fr/search?q=mosaic
Maintenant supprimons le serveur de cache n°1. La distribution des URLs est la suivante :
- Serveur de cache n°2 :
http://www.altavista.fr/search?q=gopherethttp://www.altavista.fr/search?q=netscape - Serveur de cache n°3 :
http://www.altavista.fr/search?q=operaethttp://www.altavista.fr/search?q=mosaic
On constate que la distribution des URLs précédente a très peu été boulversée. Seules les URLs dont avait la charge le
serveur de cache n°1 ont été redistribuées. Le gros serveur™ n’est sollicité que pour la clé http://www.altavista.fr/search?q=gopher.
Essayons de pousser encore le vice. Comment faire pour que lorsqu’un serveur de cache est supprimé, on ne doive pas
solliciter du tout le gros serveur™ ?
Simplement en dupliquant les responsabilités. Par exemple, on peut décider de chercher soit le serveur de cache le plus
proche dans le sans horaire OU dans le sens inverse. Ainsi l’URL http://www.altavista.fr/search?q=netscape peut
être servie par le serveur de cache n°2 ou le serveur de cache n°1.
On peut aussi décider de répliquer N fois la responsabilité d’une URL, le load-balancer peut utiliser la formule magique :
angle-du-cercle = hash(URL + (random N)) modulo 360
Une URL peut donc se retrouver à N positions différentes sur le cercle, et potentiellement être prise en charge par N serveurs de cache différents.
Avec un peu d’imagination, plein d’autres stratégies de réplication peuvent être implémentées.
On s’apperçoit que l’élément crutial de cet algorithme est la distribution des serveurs de ce cache sur le cercle. C’est la fonction de hashage qui en est responsable. L’algorithme de hashage doit avoir une très bonne distribution. Notre exemple ne comporte que trois serveurs de cache, mais on peut remarquer la proximité géographique du serveur de cache n°1 et du serveur de cache n°2. Dans l’idéal, ces trois serveurs de cache se situent à une distance de 120° l’un de l’autre.
Il serait catastrophique d’avoir nos trois serveurs séparés de quelques degrés seulement. La charge serait très mal distribuée.
Si vous utilisez le langage Java, je vous déconseille d’utiliser la fonction Object.hashcode() qui a une très
mauvaise distribution car "serveur2".hashCode() = "serveur1".hashCode() + 1.
D’un autre côté, les fonctions de hashage cryptogragraphique, telles que SHA1 ou MD5 bien qu’ayant une très bonne
distribution, avec peu de collisions, sont coûteuses en CPU.
Je conseille d’utiliser des fonctions de hashages plus légères, telle que Murmur, qui offre une bonne distribution, peu de collisions et est très rapide. Voir aussi cette réponse sur stackexchange qui compare différentes fonctions de hashage non cryptographiques.
On ne peut pas se quitter sans essayer d’implémenter un hashage consitant ! Voici quelques lignes de Clojure qui implémentent très simplement ce que j’ai décrit ci-dessus.
(defprotocol ConsistentHashRing
(add-node [this node] "add node to the ring")
(remove-node [this node] "remove node and its replicas of the ring")
(find-node [this data] "find the node responsible of data"))
(defn- find-closest-key [xs h]
(or (first (drop-while #(> h %) xs))
(first xs)))
(extend-protocol ConsistentHashRing
PersistentTreeMap
(add-node [this node] (assoc this (.hashCode node) node))
(remove-node [this node] (dissoc this (.hashCode node)))
(find-node [this data] (this (find-closest-key (keys this) (.hashCode data)))))
L’implémentation est en Clojure, je suis désolé si ça vous déboussole, mais c’est un langage qui m’est cher et que je ne peux m’empêcher d’utiliser quand je ne suis pas contraint à ne pas le faire.
Pour cette implémentation, j’ai abstrait un peu les concepts. Un serveur de cache est appelé node, les URLs sont
juste de la data.
Tout d’abord on définit un protocol (en clojure un protocol est une espèce d’interface) appelé ConsistentHashRing.
Il y a trois fonctions. add-node nous permettrait d’ajouter un serveur de cache,
remove-node d’en supprimer un et find-node de trouver un serveur de cache.
J’ai choisi d’implémenter le protocol sur une classe existante dans Clojure : PersitentTreeMap. Il s’agit
d’une implémentation d’une hashmap qui permet d’itérer sur les clés dans leur ordre naturel. En Java il s’agirait
de la classe TreeMap.
L’implémentation de add-node associe le hashCode de node à node. Contrairement à mes conseils j’utilise
Object.hashCode() comme fonction de hashage :(
L’implémentation de remove-node est triviale. Elle supprime la clé dont la valeur est le hashCode de node.
Enfin, find-node cherche le node le plus proche de la data que l’on cherche.
Cette implémentation est triviale, après tout elle ne fait que 13 lignes ! Mais je trouve qu’elle démontre bien la simplicité des concepts du hashing consistant.
Vous pouvez essayer d’implémenter les réplications par dessus. Ou utiliser un autre langage ! Je serais ravi de faire une relecture de code ;)
Sortons maintenant de notre contexte initial, à savoir le load-balancer et les servers de cache. Que peut-on inventer grâce au hashage consistant ? Allez, je vous aide un peu :
- On peut faire un filesystem distribué tolérant aux pannes
- On peut faire une base de donnée mémoire distribuée (j’ai mis le lien qui explique le partitionnement des données)
- On faire une autre base de donnée mémoire distribuée (j’ai mis le lien qui explique ce qu’est un vBucket)
- On peut faire index distribué des fichiers qui sont partagés sur Emule (la notion de noeud le plus proche est toutefois plus compliquée !)
En fait dès que vous entendez parler d’une technologie qui met les mots : distributed, autoscaling, resiliant, et replication dans la même phrase, elle utilise sans doute un hashing consistant sous le capot.