Blog de Jérôme Prudent
Développeur ...

Observation des Cache Lines

Introduction

Dans cet article je vais vous parler des performances des programmes liées aux accès à la RAM.

J’utilise la microarchitecture Sandy Bridge d’Intel sur lequel est monté un CPU i7 2600K dont je suis l’heureux possésseur.

Architecture du CPU et des mémoires

Le CPU

L’i7 a 4 coeurs et 8 threads. Cela signifie :

Linux abstrait cela en considérant 8 CPUs. (faire cat /proc/cpuinfo pour vérifier)

Les zones mémoire par core

Pour chaque core, on a ces zones :

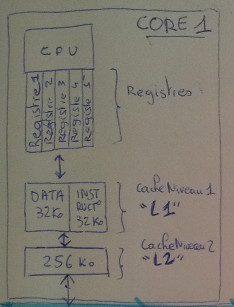
alt mémoire par core

Il y a 3 zones mémoires :

Les zones mémoires partagées par tous les Cores

Ensuite, partagées par tous les cores, on a cela :

alt mémoire partagée par les cpus

Le ring sert de bus de communication entre les coeurs et le cache de niveau L3 ou la RAM.

Voir aussi ce super schéma issu d’une présentation de Mr. T.

Deux notions importantes

D’un point de vue temps d’exécution, ce qu’il faut retenir c’est que plus les données sont proches du CPU, plus ça dépote !

L’expérience

Le programme java

    package jprudent.CacheLine;

    public class Ex2 {

        private static final int size = 512*1024*1024;
        private static final long[] array = new long[512*1024*1024];

        private static void benchMeLinear(int pas){
            System.out.print(pas + "\t");
            long start = System.nanoTime();
            for(int i=0; i<size; i+=pas){
                array[i] = i * 3;
            }
            long end = System.nanoTime();
            System.out.println((end-start) / 100000);
        }

        public static void  main(String ... args) {
            System.out.println("#Taille du tableau : " + size);
            for(int i = 1; i<1024; i+=1){
                benchMeLinear(i);
            }
        }
    }

On crée un gros tableau de 4Go que l’on met en RAM. Puis on le remplit linéairement N fois, en sautant N cases à chaque fois.
A chaque parcours, on affiche le temps d’exécution.

Au premier parcours, le pas vaut 1, le tableau est intégralement remplit.
Au second, le pas vaut 2, on remplit une case sur 2.
Au troisième, le pas vaut 3, on remplit une case sur 3.
…

Résultats

On exécute le programme:

java -Xmx8G jprudent.CacheLine.Ex2 > linear.dat

On génère un petit graphique avec gnuplot :

gnuplot> set logscale x 2
gnuplot> plot "linear.dat" using 1:2

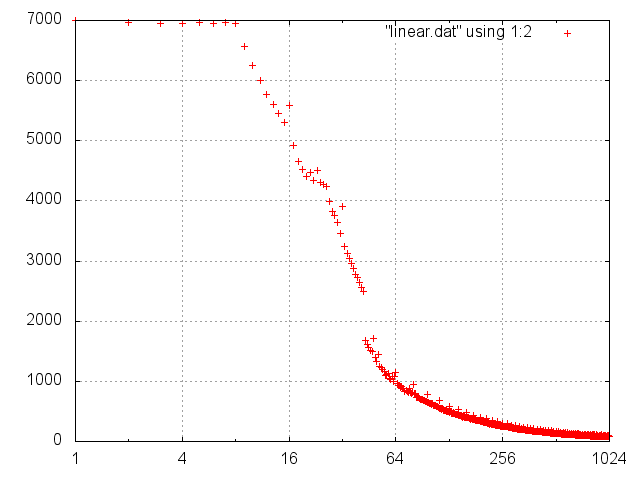
alt Résultat avec JIT

Le temps de parcours est constant de 1 à 8. Si le programme parcourt toutes les valeurs ou s’il ne parcourt qu’une valeur sur 8, le résultat est identique.

Après 8, le temps de parcours devient proportionnel au nombre de valeurs parcourues.

i * 3 n’a pas d’influence sur le temps d’exécution, sinon ce ne serait pas plat jusqu’à 8. Reste le coût d’accès à la mémoire. Il est aussi coûteux de parcourir linéairement N valeurs que N/8 valeurs.

Pourquoi 8 ?

J’ai mentionné que n’importe quelle information issue de la RAM doit au moins passer par le cache L1.

Détail important : les informations ne sont pas copiées octet par octet depuis la RAM vers le cache mais carrément par bloc de 64 octets contigüs mis en cache. Ces blocs de 64 octets s’appellent cache line.

Dans le cas du parcours du tableau avec un pas de 1:

  1. Quand i = 0, l’instruction array[0] = 0 * 3 nécessite les étapes suivantes :
    1. On doit charger dans le cache les 8 premiers octets du tableau (1 long fait 8 octets) de la RAM vers le cache. On va dire que c’est l’addresse 0 (@0x00)
    2. en fait ce sont 64 octets qui sont copiés de la RAM vers le cache, la cache line couvrant les adresses 0x00 à 0x3F.
    3. affecter la valeur 0 à @0x00
  2. Quand i = 1, l’instruction array[1] = 1 * 3 nécessite les étapes suivantes :
    1. L’adresse @0x08 est déjà dans le cache (on l’a chargée en 1.1)
    2. affecter la valeur 3 à @0x08
  3. …
  4. Quand i = 7, l’instruction array[7] = 7 * 3 nécessite les étapes suivantes :
    1. L’adresse @0x38 est déjà dans le cache (on l’a chargée en 1.1)
    2. affecter la valeur 21 à @0x38
  5. Quand i = 8, l’instruction array[8] = 8 * 3 nécessite les étapes suivantes :
    1. On doit charger l’adress 0x40 pour écrire dedans. Or, cette zone n’est pas encore remontée de la RAM
    2. en fait ce sont 64 octets qui sont copiés de la RAM vers le cache, la cache line couvrant les adresses 0x40 à 0x79.
    3. affecter la valeur 24 à @0x40

Un long fait 8 octets. Une cache line fait 64 octets, donc on a besoin d’accèder à la RAM tous les 8 indices seulement. Une fois qu’un indice est accessible dans le cache, les 7 suivants sont aussi accessibles quasiment gratuitement.

Dans le cas ou le pas vaut entre 1 et 8 il faudra monter de la RAM vers le cache l’intégralité du tableau. Et puisque monter des infos de la RAM vers le cache prend 99% du temps, pour un pas de 1 à 8, le temps d’exécution est identique. Pour les autres cas, certaines parties du tableau ne sont jamais montées en cache. D’où le rapport temps / valeur du pas.

Cet article est bien inspiré de cet original Au cas où vous n’auriez pas compris mes explications, voici la traduction de l’original:

La raison derrière tout ceci est que le CPU n’accède pas à la mémoire octet par octet. La mémoire est lue sous forme de blocs de 64 octets, appelés cache lines. Quand on lit une zone de la RAM, la cache line est intégralement récupérée de la RAM et mise en cache. Du coup, accéder aux autres valeurs appartenant à la mếme cache line est peu coûteux. Puisque 8 longs prennent 64 octet (taille d’un cache line), les boucles avec un pas de 1 à 8 doivent manipuler le même nombre de cache line: toutes les cache lines du tableau ! Mais dès que le pas est de 16, on ne doit toucher qu’une cache line sur 2, et avec un pas de 32 seulement une cache line sur 4.

Conclusion

Références et inspirations